Conceptos básicos de probabilidad.

Introducción

En varios aspectos de la diligencia humana se trabajan fenómenos que poseen algún grado de duda y en un importante número de situaciones se llega a decisiones basadas en el estudio de tales hechos. 

La duda se presenta debido a la aleatoriedad del fenómeno que se observa, pero además por el desconocimiento del verdadero estado del sistema lo cual equivale a ignorar los parámetros que determinan ese estado de la naturaleza. 

Existe duda, por ejemplo cuando: El agricultor se interesa sobre cuantas semillas serán vanas. El jefe de producción debe detener o no el proceso de producción. Al sociólogo le interesa de un conglomerado sus ingresos, estado civil, edad, etc. 

El ingeniero electrónico debe identificar la confiabilidad de un sistema. Se requiere por lo tanto de un procedimiento estructurado, sistematizado, formalizado, es decir, científico, para manejar la incertidumbre y que además permita cuantificar los diversos niveles de ésta. 

El ser humano ha tratado de medir su nivel de duda, tal medida se conoce como probabilidad.  

Conceptos básicos

Espacio muestral y eventos.

Experimentos Aleatorios  y Espacios Muestrales 

Un experimento es una observación de un fenómeno que ocurre en la naturaleza. Tipos de experimentos:

Experimentos Determinísticos: Son aquellos en donde no hay incertidumbre acerca del resultado que ocurrirá cuando éstos son repetidos varias veces. 

Experimentos Aleatorios: Son aquellos en donde no se puede anticipar el resultado que ocurrirá, pero si se tiene una completa idea acerca de todos los resultados posibles del experimento cuando éste es ejecutado.

Espacio Muestral

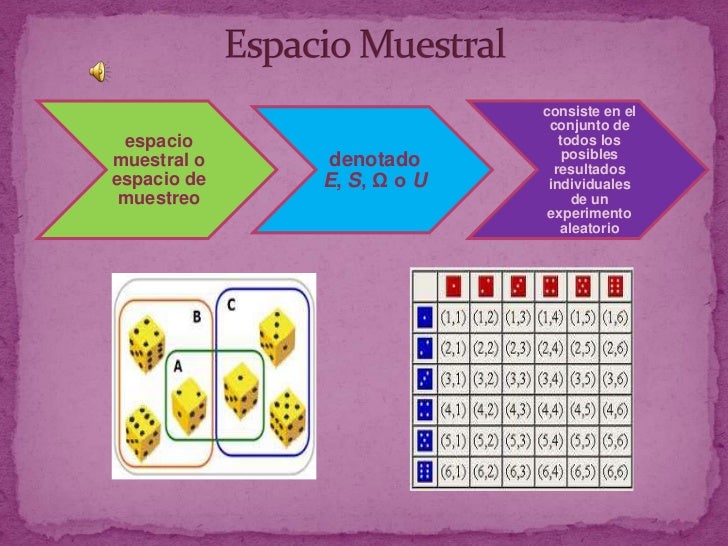
Es el conjunto de posibles resultados de un experimento aleatorio. Representaremos el espacio muestral S y cada elemento de él es llamado un punto muestral. 

Ejemplo: Lanzar un par de monedas y anotar el resultado que sale.

Tipos de espacios muestrales: 

Espacios muestrales discretos: Son espacios muestrales cuyos elementos resultan resultan de hacer conteos conteos, y por lo general general son subconjuntos subconjuntos de los números números enteros. 

Espacios muestrales continuos: Son espacios muestrales cuyos elementos resultan de hacer mediciones y por lo general son intervalos en la recta real.

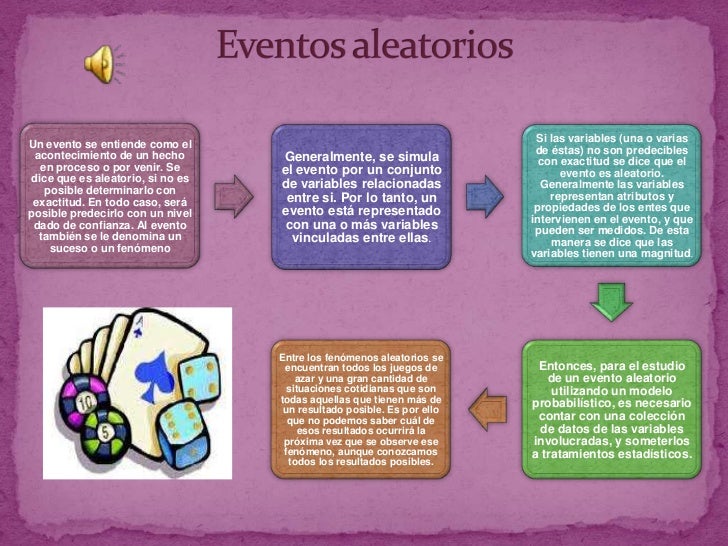
Eventos

Un Evento es un resultado particular de un experimento aleatorio. En términos de conjuntos, un evento es un subconjunto del espacio muestral. Por lo general se le representa por las primeras letras del alfabeto. Ejemplo: 

A: Que sal ga un número par al lanzar un dado.

E: Que haya que esperar más de 10 minutos para ser atendidos. 

Evento Nulo: Es aquél que no tiene elementos elementos. Se representa representa por φ. 

Evento Seguro: Es el espacio muestral que puede ser considerado como un evento.

Relaciones entre eventos

Unión de eventos: Dados dos eventos A y B de un mismo espacio muestral su unión se representa por y es el evento que contiene los elementos que á A B b El i l d l d A ∪B est án en A o en B, o en am bos. El evento ocurre si a l menos uno d e los dos eventos ocurre. Dada una colección de eventos, su unión denotada por ocurre si al menos uno de los ocurre. U n i Ai =1 A A n ,..., 1 A,(1 i n) i ≤ ≤ 

Intersección de eventos: Dados dos eventos A y B de un mismo espacio muestral su intersección se representa por y es el evento que contiene l l á A B l i i El A ∩ B los e lementos que est án en A y B a l mismo tiempo. El evento ocurre cuando los eventos ocurren simultáneamente. Dada una colección de eventos, su intersección denotada por ocurre si todos los eventos ocurren a la vez A An , ..., 1 I n i Ai =1 eventos A ,(1≤ i ≤ n) ocurren a la vez.

Evento Complemento: El complemento de un evento A se representa representa por A y es el evento que contiene contiene todos los elementos que no están en A. El evento ocurre si A no ocurre. A A 

Propiedades de relaciones entre eventos: 

Sean A, B y C elementos de un mismo espacio muestral S entonces: 

1) Propiedad Conmutativa: A ∪ B = B ∪ A A ∩ B = B ∩ A

2) Propiedad Asociativa:  ∪ (B ∪ C) = (A ∪ B) ∪ C A ∩ (B ∩ C) = (A ∩ B) ∩ C

3) Propiedad Distributiva: , A ∪ B = B ∪ A A ∩ B = B ∩ A A ∪ (B ∪ C) = (A ∪ B) ∪ C A ∩ (B ∩ C) = (A ∩ B) ∩ C A ∪(B ∩ C) =(A ∪ B)∩(A ∪ C) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) 

4) Leyes de De Morgan:A ∪ B = A ∩ B A ∩ B = A ∪ B .

Todas estas propiedades se pueden aplicar a más de dos eventos

Métodos de asignar asignar Probabilidades

Método Axiomático: La Probabilidad es considerada considerada como una función de valor real definida sobre una colección de eventos de un espacio muestral S que satisface los siguientes axiomas:

1. P(S)=0

2 Si A es un evento de S entonces P(A) ≥ 0.

Experimentos aleatorios:   Los fenómenos o experimentos aleatorios son los que al repetirlos en análogas condiciones, pueden dar lugar a varios resultados diferentes, sin que pueda ser previsible enunciar con certeza cuál de estos se va a obtener en la realización del experimento. Como lanzar una moneda, sacar una carta de la baraja, ganar la lotería, sacar una bola de una urna, etc.

Sucesos:  Suceso de un fenómeno aleatorio es cada uno de los subconjuntos del espacio muestral  . Para designar cualquier suceso, también llamado suceso aleatorio, de un experimento aleatorio utilizaremos letras mayúsculas. Al conjunto de todos los sucesos que ocurren en un experimento aleatorio se le llama espacio de sucesos y se designa por   S.

Ejemplo:  En el ejemplo anterior, son subconjuntos de  E:

Salir múltiplo de 5:   E={5,10}. 

Salir número primo:   E={2,3,5,7,11}. 

Salir mayor o igual que 10:      E={10,11,12}.  

Tipos mas frecuentes de sucesos:

Sucesos elementales son los que están formados por un solo resultado del experimento.

Sucesos compuestos son los que están formados por dos o más resultados del experimento; es decir, por dos o más sucesos elementales.

Suceso seguro es el que se verifica al realizar el experimento aleatorio. Está formado por todos los resultados posibles del experimento y, por tanto, coincide con el espacio muestral.

Suceso imposible es el que nunca se verifica. Se representa por  Ø.

Operaciones con sucesos

 Inclusión e igualdad de sucesos: Un suceso A esta incluido (contenido) en otro suceso B si todo suceso elemental de A pertenece también a B. Se representa por A(C. Dos sucesos A y B son iguales si están formados por los mismos sucesos elementales. Se representa por A=B. 

Unión de sucesos: Si tenemos dos sucesos A y B de un mismo experimento aleatorio, llamamos suceso unión de A y B  al suceso que se realiza cuando lo hacen A o B. Cuando   es el suceso imposible, decimos que los sucesos  A y B son incompatibles. Cuando no sucede esto, decimos que  A y B  son compatibles.

Intersección de sucesos: Si tenemos dos sucesos A y B de un mismo experimento aleatorio, llamamos suceso intersección de A y B al suceso que se realiza cuando lo hacen A y B. Se representa por  .

Sucesos contrarios: 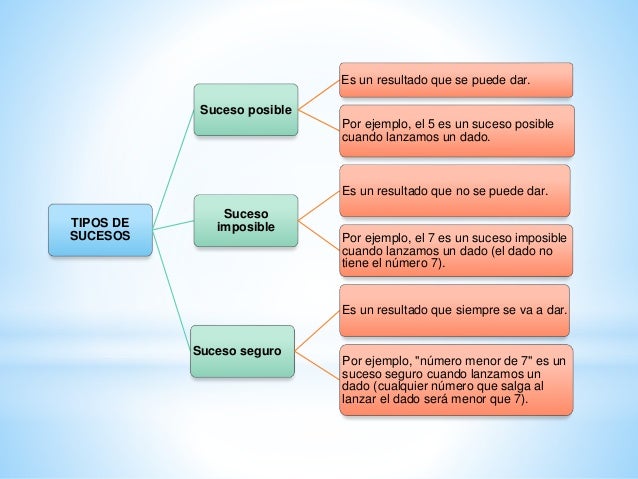Cuando la unión de dos sucesos es el espacio muestral y la intersección de los mismos conjuntos da el conjunto imposible, decimos que ambos sucesos son complementarios o contrarios. Para un suceso cualquiera A de un experimento aleatorio, llamamos suceso contrario del suceso A  al suceso que se verifica cuando no se verifica A, y recíprocamente.

Tipos de sucesos

·         Exhaustivo: se dice que dos o más sucesos son exhaustivos si se consideran todos los posibles resultados.

Simbólicamente: p (A o B o...) = 1

·         No exhaustivos: se dice que dos o más sucesos son exhaustivos si no cubren todos los posibles resultados.

·          

·         Mutuamente excluyentes: sucesos que no pueden ocurrir en forma simultánea:

P(A y B) = 0 y p(A o B) = p(A) + p (B)

Ejemplo: hombres, mujeres

·         No mutuamente excluyentes: sucesos que pueden ocurrir en forma simultánea:

P (A o B) = p (A) + p (B) – p (A y B )

Ejemplo: hombres, ojos cafés

·         Independientes: Sucesos cuya probabilidad no se ve afectada por la ocurrencia o no ocurrencia del otro :

P ( AI B ) = P ( A ); P ( BIA ) = P (B) Y P (A Y B) = P(A) P(B)

Ejemplo: sexo y color de ojos

·         Dependientes: sucesos cuya probabilidad cambia dependiendo de la ocurrencia o no ocurrencia del otro.

Conclusión

Los conceptos antes mencionados han sido analizados e investigados de tal manera que fuera fácil su comprencion ya que la estadística es la ciencia que trata de entender organizar y tomar decisiones que estén de acuerdo con lo análisis efectuados.

Bibliografia

http://academic.uprm.edu/eacuna/miniman4sl.pdf
https://es.khanacademy.org/math/probability/independent-dependent-probability/basic-probability/a/probability-the-basics
http://www.ingenieria.unam.mx/calyesd/Docs/docs_proEsd/Notas_proEsd/Conceptos_Proba_Est.pdf